01 Image Formation
约 1688 个字 预计阅读时间 6 分钟
相机与透镜¶
最简单的相机模型是利用小孔成像实现的,我们称之为针孔相机模型(Pinhole Camera Model, PCM)。如下图,我们在物体与成像面之间,添加一个障碍物来挡住大部分光线,从而使得成像面上的点和物体上的点是近似“一一对应”的。如果没有添加障碍物,那么物体上的不同的点反射的光线会在成像面上重合,导致成像的模糊。
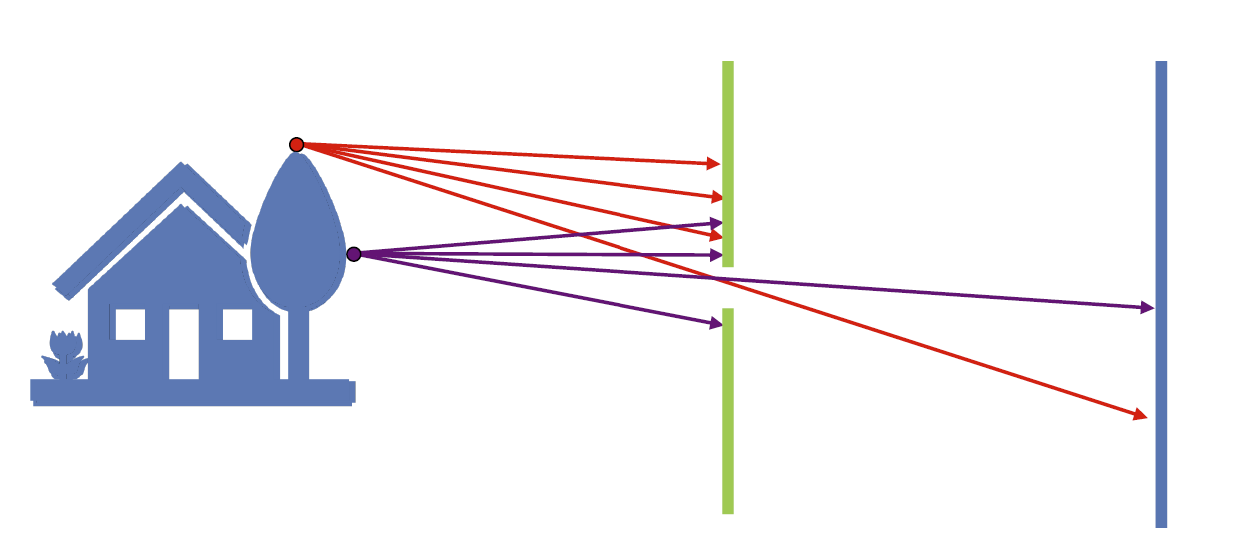
我们称这个障碍物上面的小孔为光圈(aperture)。按照之前的叙述,看起来光圈越小,越能在成像面上保持物体的原始形状,但是它并不是越小越好。其原因主要有两个:一方面,光圈越小,通过的光越少,成像会变得越弱;另一方面,光圈越小,或者说越接近于可见光的波长,衍射就越明显,同样会导致成像的模糊。其效果可以在下面一张图中体现:

为了解决光圈导致的光通量减少的问题,我们采用透镜(lens)来代替一部分小孔的功能,它具备小孔的成像特性,但是可以收集更多的光线。当然,物距 \(o\) 、像距 \(i\) 和焦距 \(f\) 之间的关系为:
如果 \(o \rightarrow \infty\) ,则 \(f \rightarrow i\) 。这个式子可以很轻松地通过几何光学方法导出,在此略去。
对焦距的改变可以被视作一种缩放,它与视野(field of view, FOV)有关。我们所谓的视野就是在传感器上所能看到的物体的范围,其与焦距的关系如下图:
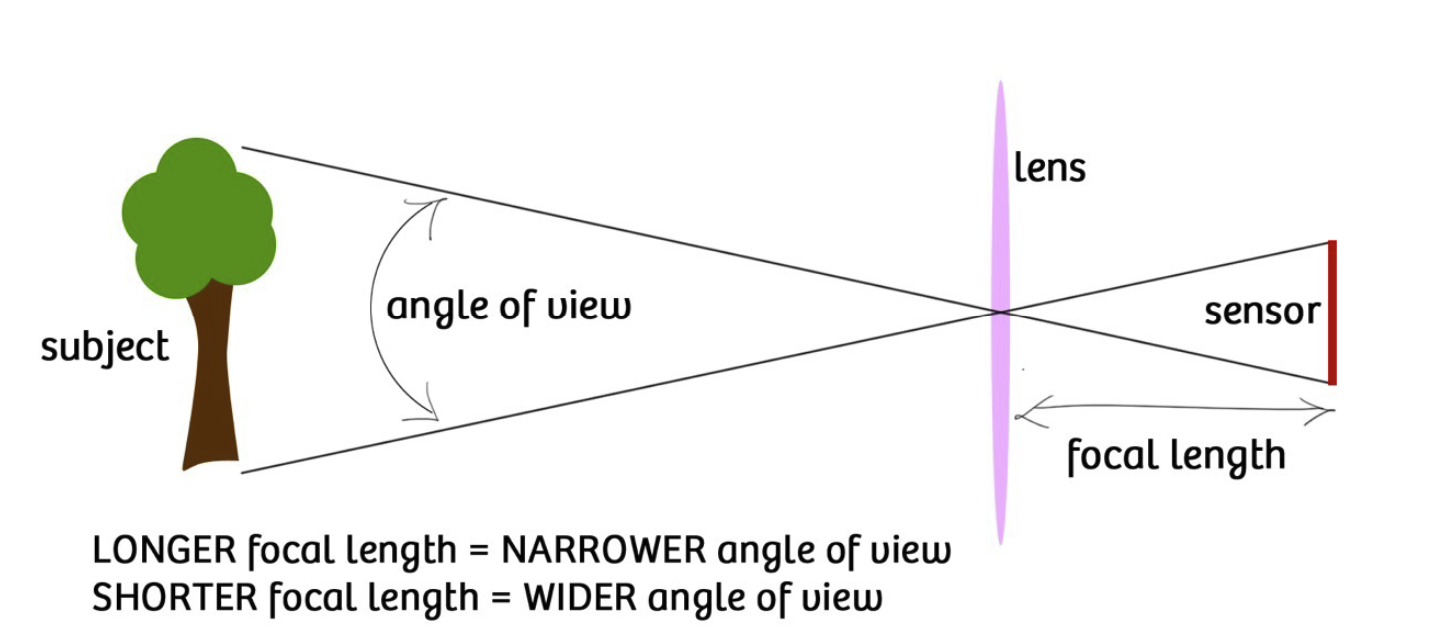
在上图中,我们同样发现,视野也和传感器大小(sensor size)有关,传感器越大,视野也就越大。
在透镜的模型中,我们的光圈就变成了仅控制光的通量的设备,如下图中的 \(D\) 标记的就是光圈的直径:
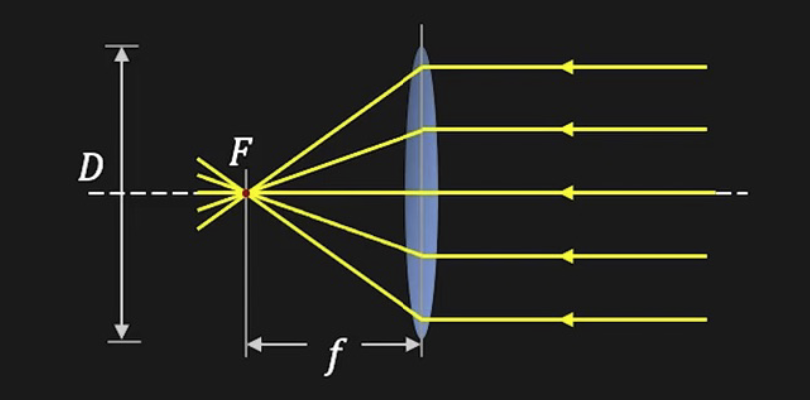
一种更加方便的做法是,直接用焦距为单位表示光圈的直径,这就是所谓的 F-数(F-number ,或称光圈数):
透镜将一点发出的光汇聚到一点,因此不可避免地会出现对应的点不在成像面上的情形,这种现象被我们称为失焦(defocus)。通过一点点几何推导可以计算,模糊圈(blur circle,即成像面上一点的像的集合)的直径为:
其中 \(i\) 为实际像距,\(i'\) 为理论像距,\(D\) 为光圈大小。
于是我们可以引出景深(depth of field, DoF)的概念。我们称图像“足够聚焦”的物距范围为景深,在这些点上,模糊圈的直径小于像素大小,因此失焦没有影响最终的成像结果。同样通过一些几何推导可以得到:
几何图像生成(geometric image formation)¶
几何图像生成描述的是从三维世界到二维图像的投影。我们的相机模型描述的就是这个过程,接下来,我们将使用投影的方式来描述这一点。考虑三维点:
在二维平面上被投影到:
为了更好地描述它们之间的关系,我们采用齐次坐标(homogeneous coordinates)。其转换方式就是对原先坐标加上一行 \(1\) ,即:
反过来的转换是除去扩张的那一列:
这种方式定义的坐标很显然对伸缩不变,从代数的角度看,它就是一个商掉某种等价关系的欧氏空间,这个等价关系定义为:
欧氏空间视作 \(\mathbb R\) 上的线性空间 \(V\) ,则与之对应的射影空间 \(\mathbf P (V) = (V - \{0\}) / \sim\)。
在这种情形下,我们就可以将投影表示成一种线性变换:
注意,在原始情形下,这种变换从根本上就不是线性的。因此,我们取齐次坐标的含义就是把投影“变成”线性的,这通过丢弃原有坐标中的长度、角度信息来完成。
通过这种视角,我们可以更进一步地理解投影的含义。它将直线映到直线,但不保长也不保角,事实上,长度和角度信息在射影几何中就是不必须的,从这个视角可以更好地理解投影操作。
对于这种不保角性的一个很好说明是灭点(vanishing point)的存在。一族平行线在被投影之后收缩于同一点,这个点与相机的连线恰与这族直线平行,如图:
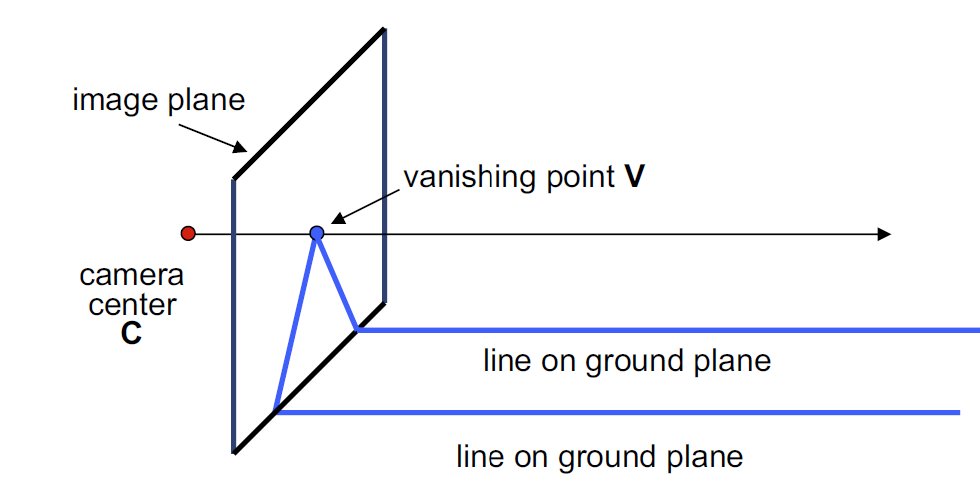
在空间中,任意一组平行线的灭点都在同一条直线上,我们称之为灭线(vanishing line)。这几个结论的证明在此略去。
在建筑摄影的过程中,投影经常带来不好的效果。倾斜相机会导致竖直线聚于一点,而直接平视拍摄会导致相机只能捕捉到建筑的最下方部分;而如果将透镜向上移,则能捕获完整的水平图像,其数学原理由 Scheimpflug 原理描述,在此不作展开。
另一种投影的问题由达芬奇指出。在使用它拍摄一组平行的栏杆时,越靠近画面外侧的栏杆会显得越粗。这种形变(distortion)是由于投影原理自身。不理想的透镜则会导致另外两种径向(radical)的形变,即枕形畸变(pin cushion)和桶形畸变(barrel)。
在投影矩阵中取 \(f = 1\) ,我们可以得到正交投影(orthographic projection)的描述。这种投影发生于相机到成像面的距离为无穷时,表现为单纯地“压缩”了 \(z\) 坐标,将 \((x, y, z)\) 映到 \((x, y)\),这是投影的一种特殊情形,其灭点和灭线都在无穷远处。
光度图像生成(photometric image formation)¶
下面我们来描述三维世界到二维图像的色彩关系。
Error
未完成!